Distributed Lag Linear and Non-Linear Models in R: The Package dlnm

Tip

Distributed lag/non-linear models (DLNMs) is a modelling framework to describe simultaneously a non-linear and a delayed effects between predictors and an outcome, a dependency defined as exposure-lag-response (outcome) association in time series data. This methodology rests on the definition of a crossbasis, a bi-dimensional functional space expressed by the combination of two sets of basis functions, which specify the relationships in the dimensions of predictor and lags, respectively (Gasparrini 2011).

What is DLNM?

# Read the instruction of the package
vignette("dlnmOverview")
vignette("dlnmExtended")
vignette("dlnmTS")

In case of protracted exposures, the data can be structured by the partition in equally-spaced time periods, defining a series of exposure events and outcomes realizations. This methodology allows the effect of a single exposure event to be distributed over a specific period of time, using several parameters to explain the contributions at different lags, thus providing a comprehensive picture of the time-course of the exposure-response relationship.

“Non-linear” Relationship: The link between exposure and outcome might not be a straight line. Maybe very high temperatures drastically increase health risks, while mild temperatures don’t have much effect. DLNMs use flexible curves (like splines) to model these more complex, curvy relationships.

Lagged Effects: Instead of assuming an exposure affects health only on the same day, DLNMs captures delayed effects—like a heat wave that might cause more hospital admissions not just today, but also in the following days or weeks.

Traditionally, an epidemiological approach is to study the exposure-response relationship. The DLNM framework extend it by adding the lag-response relationship to construct the so-called dependency exposure-lag-response relationship, characterized by the bi-dimensional space of predictor and lag.

Specifically, two set of basis functions are chosen independently for modelling the exposure and lag-response relationships. These are then combined through a special tensor product defined by bi-dimensional cross-basis functions. The choice of the two sets of functions determines the shape of the relationship in each dimension. DLMs can be considered special cases of the more general DLNMs, when the exposure-response is assumed linear.

In the standard definition of the DLM/DLNM modelling framework, models are fitted with common regression methods, such as generalized linear models (GLMs) or Cox proportional hazard models. The functions in the dlnm package can be used more generally to facilitate the computation and interpretation of associations estimated from regression models, beyod the specific case of distributed lag modelling. Specifically, the functions can be applied to obtain predictions and plots of point estimates and measures of uncertainty for linear or non-linear unlagged relationships, estimated from either unpenalized (e.g., GLMs and Cox models) or penalized (GAMs) models.

The first step for performing DLMs or DLNMs consists of the choice of two sets of basis functions for modelling the exposure-lag-response association. Any kind of function determining completely known parametric transformations of the predictor can be used, and several options are available in the dlnm package. All the functions are meant to be called internally by onebasis() and crossbasis() and not directly run by the users.

Since version 2.0.0 of dlnm, onebasis() simply acts as a wrapper to other functions. The function has a first argument x for the predictor variable (i.e. ambient temperature), and another argument fun for specifying the basis function to be called internally, whose arguments are passed through the ellipsis argument ‘…’.

The function crossbasis() is the main function in the package dlnm. It calls onebasis() internally to generate the basis matrices for exposure-response and lag-response relationships, and combines them through a special tensor product in order to create the cross-basis, which specifies the exposure-lag-response dependency simultaneously in the two dimensions. The class of the first argument x of crossbasis() defines how the data are interpreted. If a vector, x is assumed to represent an equally-spaced, complete and ordered series of observations in a time series framework. If a matrix, x is assumed to represent a series of exposure histories for each observation (rows) and lag (columns). The lag period can be defined through the second argument lag. The two arguments argvar and arglag contain lists of arguments, each of them to be passed to onebasis() to build the matrices for the exposure-response and lag-response relationships respectively. The additional argument group, used only for time series data, defines groups of observations to be considered as individual unrelated series, and may be useful for example in seasonal analyses.

The function crosspred(): The interpretation of estimated parameters is usually complex for non-trivial basis transformations in DLMs, and virtually impossible in bi-dimensional DLNMs. The function crosspred() facilitates the interpretation by predicting the association for a grid of predictor and lag values, chosen by default or directly by the user. The function creates the same basis or cross-basis functions for the chosen predictor and lag values, extracts the related parameters estimated in the regression model, and generates predictions with associated standard errors and confidence intervals.

Practical example

Important

We will use the chicagoNMMAPS as an example of analysis. The example refers to the effects on all-cause mortality of two environmental factors, air pollution (ozone) and temperature, in the city of Chicago during the period 1987-2000.

pacman::p_load(
  rio,
  here,
  DT,
  dlnm,
  splines,
  survival,
  sjPlot,
  tidyverse
)
data(chicagoNMMAPS)
datatable(chicagoNMMAPS)

A model for time series data may be generally represented by:

\[ g(\mu_i) = \alpha + \sum_{j=1}^J s_j\bigl(x_{ij}, \beta_j\bigr) + \sum_{k=1}^K \gamma_k\,u_{ik} \]

In the illustrative example on Chicago data, the outcome Yt is daily death counts, assumed to originate from a so-called overdispersed Poisson distribution with E(Y) = μ, V(Y) = \(\phi\) μ, and a canonical log-link. The non-linear and delayed effects of ozone and temperature are modeled through as particular functions sj which define the relationship along the two dimensions of predictor and lags. Generally, non-linear exposure-response dependencies are expressed in regression models through appropriate functions s. The main choices typically rely on functions describing smooth curves, like polynomials or spline functions. All of these functions apply a transformation of the original predictor to generate a set of transformed variables included in the model as linear terms.

Caution

The DLNMs framework introduced in this paper is developed for time series data. The general expression of the basic model in allows this methodology to be applied to any family distribution and link function within (generalized) linear models (GLM), with extensions to generalized additive models (GAM) or models based on generalized estimating equations (GEE) (Perperoglou et al. 2019). However, the current implementation of DLNMs requires single series of equally-spaced, complete and ordered data.

Specifying a DLNM

basis.o3 <- crossbasis(
  chicagoNMMAPS$o3,
  lag = 10,
  argvar = list(fun = "thr", thr.value = 40.3, side = "h"),
  arglag = list(fun = "strata", breaks = c(2, 6))
)

klag <- exp(((1 + log(30)) / 4 * 1:3) - 1)
basis.temp <- crossbasis(
  chicagoNMMAPS$temp,
  lag = 30,
  argvar = list(fun = "bs", degree = 3, df = 6),
  arglag = list(knots = klag)
)

summary(basis.o3)
CROSSBASIS FUNCTIONS
observations: 5114 
range: -0.8319944 to 65.80827 
lag period: 0 10 
total df:  3 

BASIS FOR VAR:
fun: thr 
thr.value: 40.3 
side: h 
intercept: FALSE 

BASIS FOR LAG:
fun: strata 
df: 3 
breaks: 2 6 
ref: 1 
intercept: TRUE 
summary(basis.temp)
CROSSBASIS FUNCTIONS
observations: 5114 
range: -26.66667 to 33.33333 
lag period: 0 30 
total df:  30 

BASIS FOR VAR:
fun: bs 
knots: 1.666667 10.55556 19.44444 
degree: 3 
intercept: FALSE 
Boundary.knots: -26.66667 33.33333 

BASIS FOR LAG:
fun: ns 
knots: 1.105502 3.322105 9.983144 
intercept: TRUE 
Boundary.knots: 0 30
  • The first argument x of crossbasis() is the predictor series, in this case chicagoNMMAPS\(o3 and chicagoNMMAPS\)temp. The values in x are expected to represent an equally-spaced and ordered series, with the interval defining the lag unit
  • The cross-basis for ozone comprises a threshold function for the space of the predictor, with a linear relationship beyond 40.3 μgr/m3, and a dummy parameterization assuming constant distributed lag effects along the strata of lags 0-1, 2-5 and 6-10 ().
  • In contrast, the options for temperature are a cubic spline with 6 df (knots at equally-spaced percentiles by default) centered at 25°C, and a natural cubic spline (lagtype = “ns” by default) with 5 df (knots at equally-spaced values in the log scale of lags by default), up to a maximum of 30 lags.

The cross-basis matrices can be included in the model formula of a common regression function in order to estimate the corresponding parameters η in (5). In the example, the final model includes also a natural cubic spline with 7 df/year to model the seasonal and long time trend components and a factor for day of the week, specified by the function ns() in the package splines, which needs to be loaded in the session. The code is:

model <- glm(
  death ~ basis.temp + basis.o3 + ns(time, 7 * 14) + dow,
  family = quasipoisson(),
  chicagoNMMAPS
)
  death
Predictors Incidence Rate Ratios CI p
(Intercept) 129.22 82.15 – 203.14 <0.001
basis tempv1 l1 0.91 0.81 – 1.01 0.070
basis tempv1 l2 1.03 0.97 – 1.09 0.409
basis tempv1 l3 0.98 0.91 – 1.06 0.659
basis tempv1 l4 1.02 0.91 – 1.14 0.781
basis tempv1 l5 0.99 0.92 – 1.06 0.734
basis tempv2 l1 0.95 0.88 – 1.02 0.138
basis tempv2 l2 0.99 0.96 – 1.03 0.737
basis tempv2 l3 0.99 0.95 – 1.04 0.719
basis tempv2 l4 1.04 0.96 – 1.12 0.325
basis tempv2 l5 0.97 0.93 – 1.02 0.259
basis tempv3 l1 0.88 0.82 – 0.96 0.003
basis tempv3 l2 1.00 0.96 – 1.05 0.865
basis tempv3 l3 0.98 0.93 – 1.04 0.491
basis tempv3 l4 1.02 0.94 – 1.12 0.622
basis tempv3 l5 0.98 0.93 – 1.03 0.393
basis tempv4 l1 0.91 0.84 – 0.98 0.015
basis tempv4 l2 1.00 0.96 – 1.04 0.964
basis tempv4 l3 0.96 0.91 – 1.01 0.162
basis tempv4 l4 1.10 1.01 – 1.19 0.029
basis tempv4 l5 0.94 0.90 – 0.99 0.023
basis tempv5 l1 0.76 0.70 – 0.82 <0.001
basis tempv5 l2 0.99 0.95 – 1.04 0.823
basis tempv5 l3 0.95 0.89 – 1.01 0.081
basis tempv5 l4 1.07 0.98 – 1.17 0.155
basis tempv5 l5 0.96 0.90 – 1.01 0.136
basis tempv6 l1 1.21 1.10 – 1.32 <0.001
basis tempv6 l2 0.98 0.93 – 1.03 0.470
basis tempv6 l3 0.89 0.83 – 0.95 <0.001
basis tempv6 l4 1.33 1.20 – 1.47 <0.001
basis tempv6 l5 0.86 0.80 – 0.91 <0.001
basis o3v1 l1 1.00 1.00 – 1.00 <0.001
basis o3v1 l2 1.00 1.00 – 1.00 0.007
basis o3v1 l3 1.00 1.00 – 1.00 <0.001
time [1st degree] 1.09 0.89 – 1.33 0.395
time [2nd degree] 1.17 0.90 – 1.53 0.237
time [3rd degree] 1.09 0.86 – 1.39 0.467
time [4th degree] 1.16 0.90 – 1.50 0.247
time [5th degree] 1.15 0.91 – 1.46 0.236
time [6th degree] 1.13 0.89 – 1.44 0.304
time [7th degree] 1.07 0.85 – 1.35 0.557
time [8th degree] 1.25 0.99 – 1.59 0.065
time [9th degree] 1.05 0.82 – 1.35 0.686
time [10th degree] 1.06 0.82 – 1.37 0.662
time [11th degree] 1.13 0.88 – 1.45 0.350
time [12th degree] 1.17 0.92 – 1.48 0.205
time [13th degree] 1.06 0.84 – 1.35 0.601
time [14th degree] 1.12 0.89 – 1.42 0.337
time [15th degree] 1.08 0.86 – 1.37 0.504
time [16th degree] 1.15 0.90 – 1.47 0.267
time [17th degree] 1.07 0.83 – 1.37 0.619
time [18th degree] 1.21 0.94 – 1.54 0.136
time [19th degree] 1.04 0.82 – 1.32 0.774
time [20th degree] 1.38 1.09 – 1.74 0.007
time [21st degree] 1.04 0.82 – 1.32 0.729
time [22nd degree] 1.12 0.89 – 1.42 0.338
time [23rd degree] 1.12 0.88 – 1.43 0.372
time [24th degree] 1.04 0.81 – 1.34 0.748
time [25th degree] 1.18 0.92 – 1.51 0.190
time [26th degree] 1.11 0.88 – 1.42 0.375
time [27th degree] 1.08 0.86 – 1.37 0.507
time [28th degree] 1.17 0.93 – 1.48 0.189
time [29th degree] 1.08 0.85 – 1.37 0.548
time [30th degree] 1.18 0.92 – 1.51 0.191
time [31st degree] 1.04 0.81 – 1.33 0.769
time [32nd degree] 1.16 0.91 – 1.49 0.241
time [33rd degree] 1.08 0.85 – 1.37 0.533
time [34th degree] 1.28 1.01 – 1.62 0.038
time [35th degree] 1.00 0.79 – 1.27 0.994
time [36th degree] 1.13 0.89 – 1.43 0.329
time [37th degree] 1.08 0.85 – 1.37 0.552
time [38th degree] 1.03 0.80 – 1.32 0.821
time [39th degree] 1.10 0.86 – 1.40 0.465
time [40th degree] 1.17 0.92 – 1.49 0.193
time [41st degree] 1.02 0.81 – 1.30 0.844
time [42nd degree] 1.11 0.88 – 1.41 0.363
time [43rd degree] 1.31 1.04 – 1.66 0.024
time [44th degree] 1.03 0.81 – 1.31 0.825
time [45th degree] 1.21 0.94 – 1.56 0.131
time [46th degree] 1.13 0.89 – 1.45 0.324
time [47th degree] 1.12 0.88 – 1.42 0.365
time [48th degree] 1.21 0.96 – 1.53 0.116
time [49th degree] 1.04 0.82 – 1.32 0.738
time [50th degree] 1.14 0.90 – 1.45 0.284
time [51st degree] 1.14 0.90 – 1.45 0.291
time [52nd degree] 1.07 0.83 – 1.37 0.593
time [53rd degree] 1.17 0.91 – 1.49 0.223
time [54th degree] 1.10 0.87 – 1.40 0.442
time [55th degree] 1.26 1.00 – 1.60 0.053
time [56th degree] 1.18 0.93 – 1.49 0.174
time [57th degree] 1.08 0.85 – 1.37 0.541
time [58th degree] 1.12 0.88 – 1.43 0.366
time [59th degree] 1.26 0.98 – 1.63 0.078
time [60th degree] 1.02 0.79 – 1.30 0.899
time [61st degree] 1.11 0.87 – 1.40 0.412
time [62nd degree] 1.17 0.92 – 1.48 0.193
time [63rd degree] 0.96 0.76 – 1.21 0.716
time [64th degree] 1.13 0.89 – 1.43 0.314
time [65th degree] 1.06 0.83 – 1.35 0.643
time [66th degree] 1.07 0.84 – 1.38 0.588
time [67th degree] 1.02 0.79 – 1.30 0.904
time [68th degree] 1.19 0.94 – 1.51 0.146
time [69th degree] 1.21 0.96 – 1.53 0.117
time [70th degree] 0.93 0.73 – 1.17 0.531
time [71st degree] 1.16 0.91 – 1.47 0.221
time [72nd degree] 1.02 0.80 – 1.30 0.874
time [73rd degree] 1.03 0.80 – 1.32 0.832
time [74th degree] 1.01 0.79 – 1.30 0.919
time [75th degree] 1.12 0.88 – 1.43 0.343
time [76th degree] 1.05 0.83 – 1.33 0.699
time [77th degree] 1.21 0.95 – 1.53 0.119
time [78th degree] 0.97 0.77 – 1.23 0.801
time [79th degree] 1.03 0.80 – 1.32 0.825
time [80th degree] 1.10 0.86 – 1.42 0.440
time [81st degree] 1.06 0.82 – 1.36 0.666
time [82nd degree] 1.04 0.82 – 1.33 0.726
time [83rd degree] 1.13 0.90 – 1.43 0.291
time [84th degree] 1.31 1.03 – 1.66 0.026
time [85th degree] 1.06 0.84 – 1.35 0.620
time [86th degree] 1.01 0.79 – 1.29 0.961
time [87th degree] 1.05 0.82 – 1.36 0.685
time [88th degree] 1.00 0.79 – 1.28 0.981
time [89th degree] 1.05 0.83 – 1.34 0.692
time [90th degree] 1.35 1.06 – 1.70 0.013
time [91st degree] 0.88 0.70 – 1.11 0.283
time [92nd degree] 1.14 0.90 – 1.46 0.272
time [93rd degree] 1.01 0.79 – 1.29 0.937
time [94th degree] 1.03 0.81 – 1.33 0.788
time [95th degree] 1.06 0.83 – 1.35 0.651
time [96th degree] 1.08 0.92 – 1.27 0.357
time [97th degree] 1.20 0.73 – 1.95 0.473
time [98th degree] 1.00 0.92 – 1.09 0.994
dow [Monday] 1.04 1.03 – 1.05 <0.001
dow [Tuesday] 1.03 1.02 – 1.04 <0.001
dow [Wednesday] 1.01 1.00 – 1.02 0.010
dow [Thursday] 1.02 1.01 – 1.03 0.002
dow [Friday] 1.02 1.01 – 1.03 <0.001
dow [Saturday] 1.02 1.01 – 1.03 <0.001
Observations 5084
R2 Nagelkerke 0.657

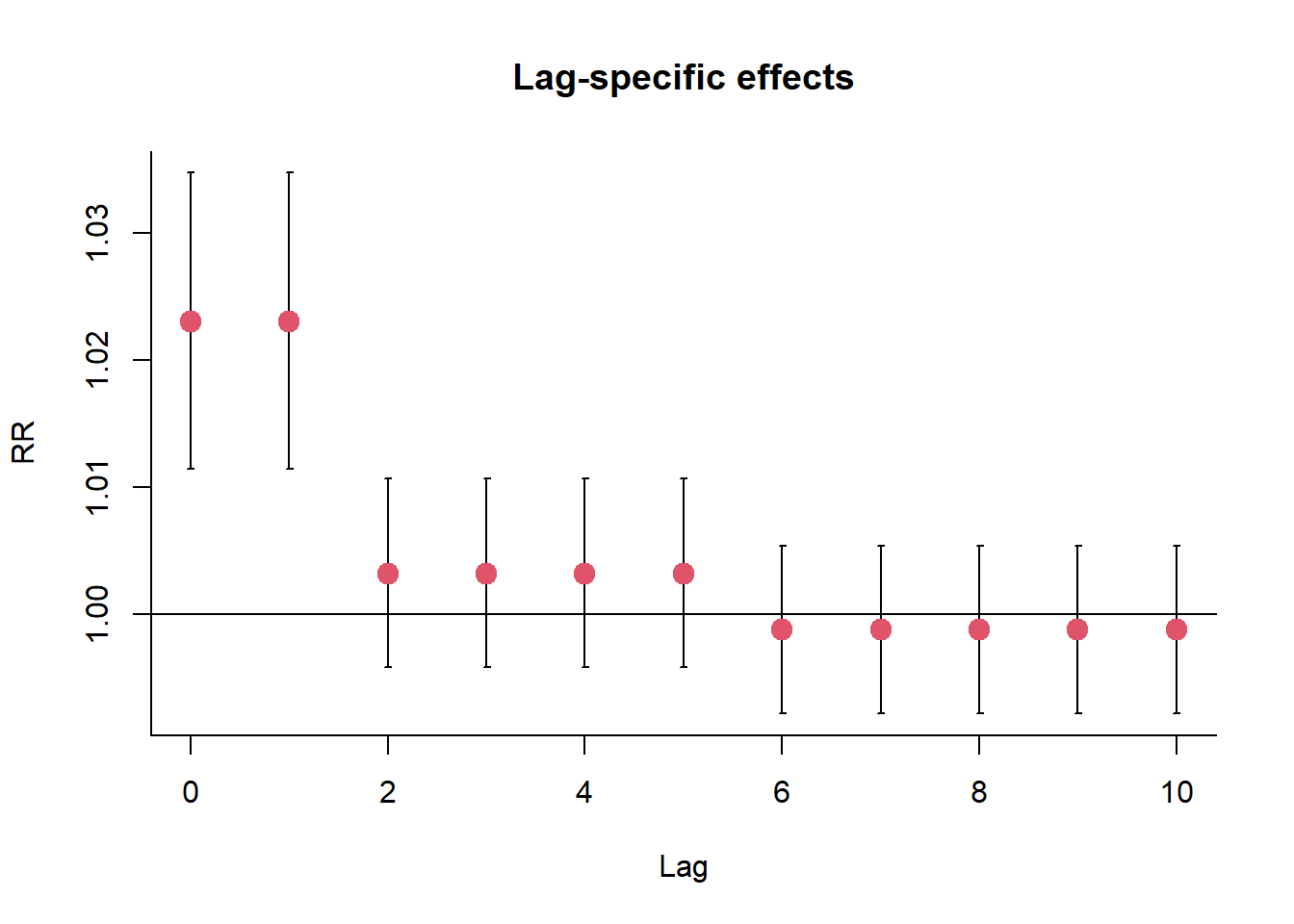
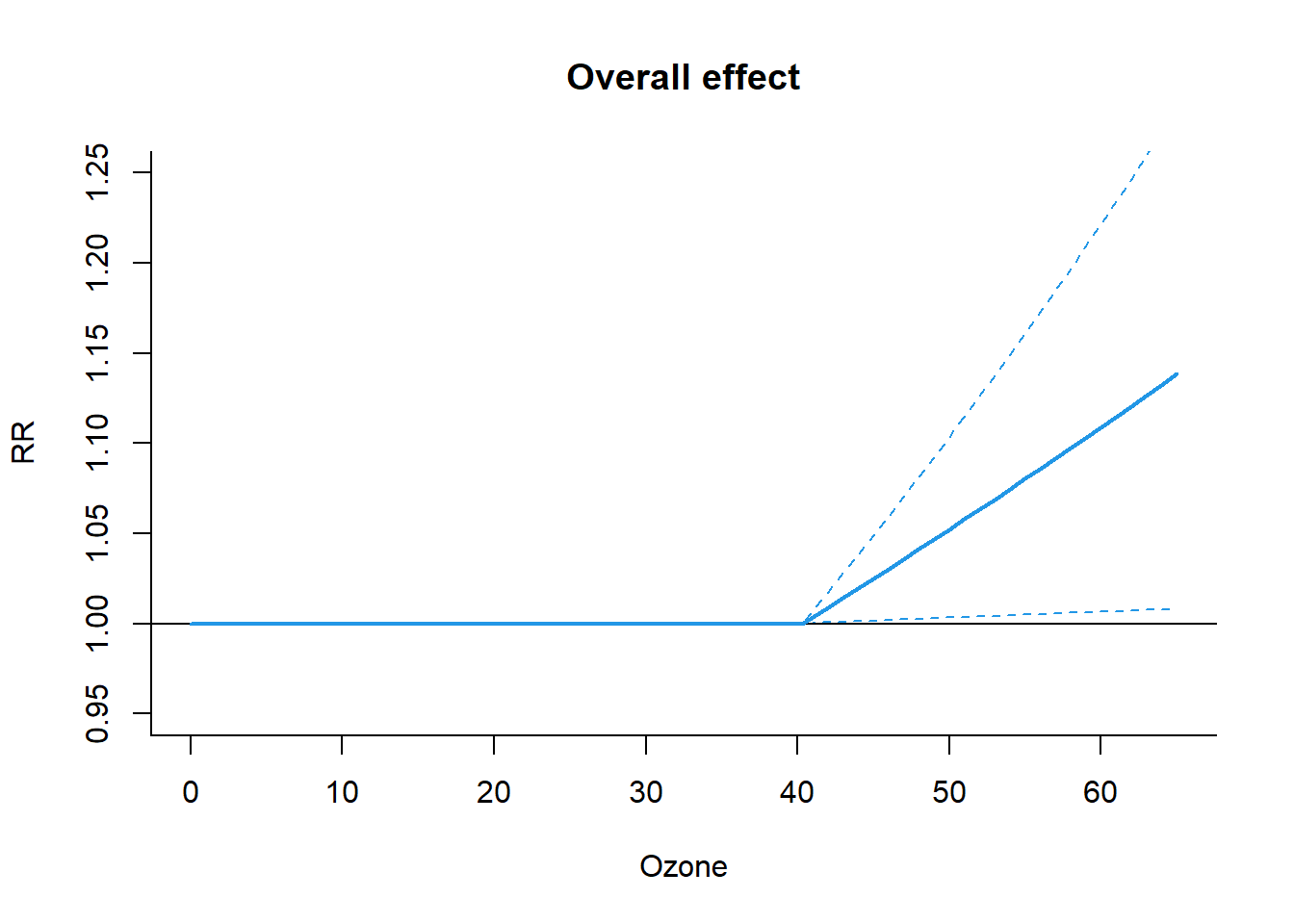
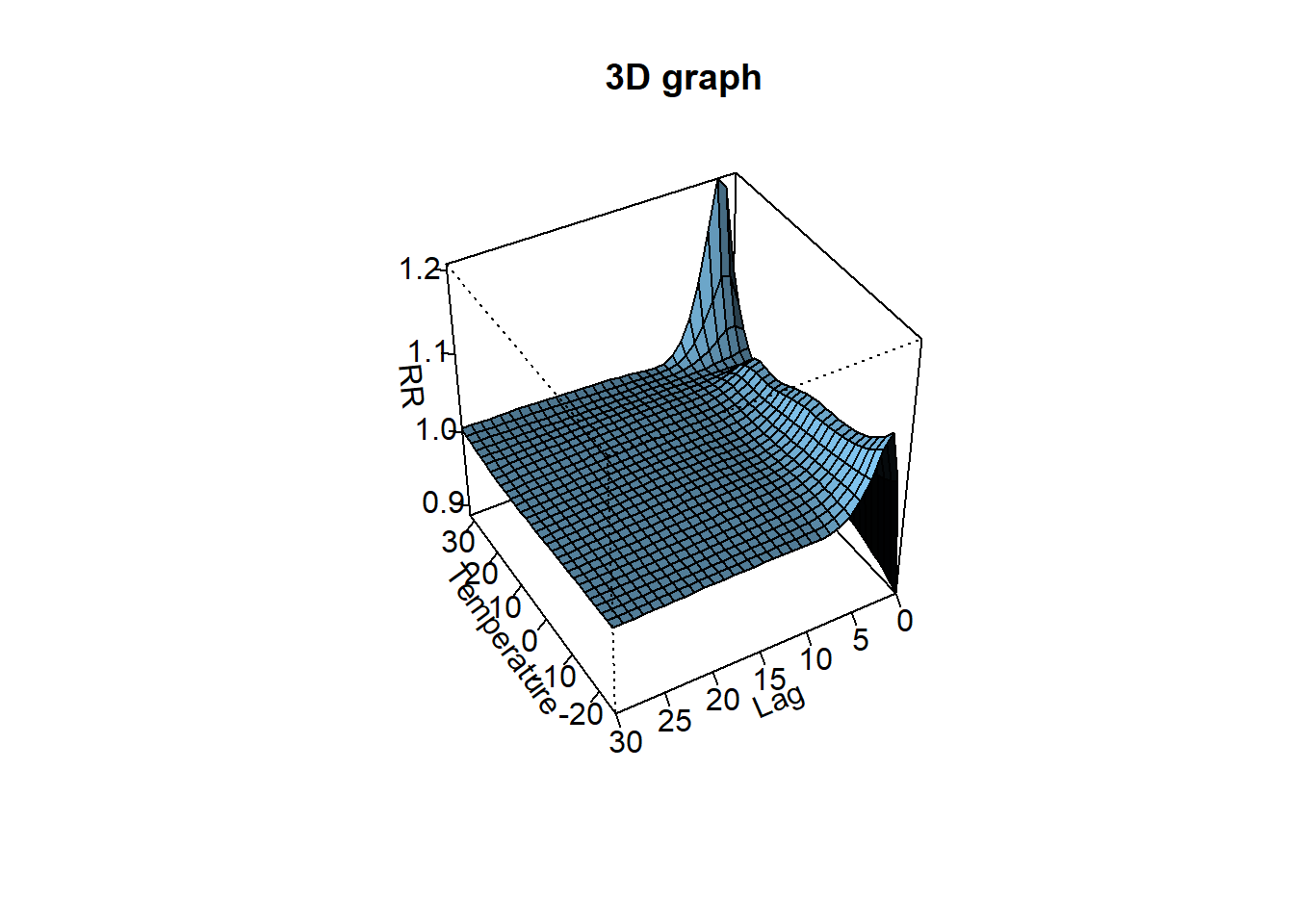
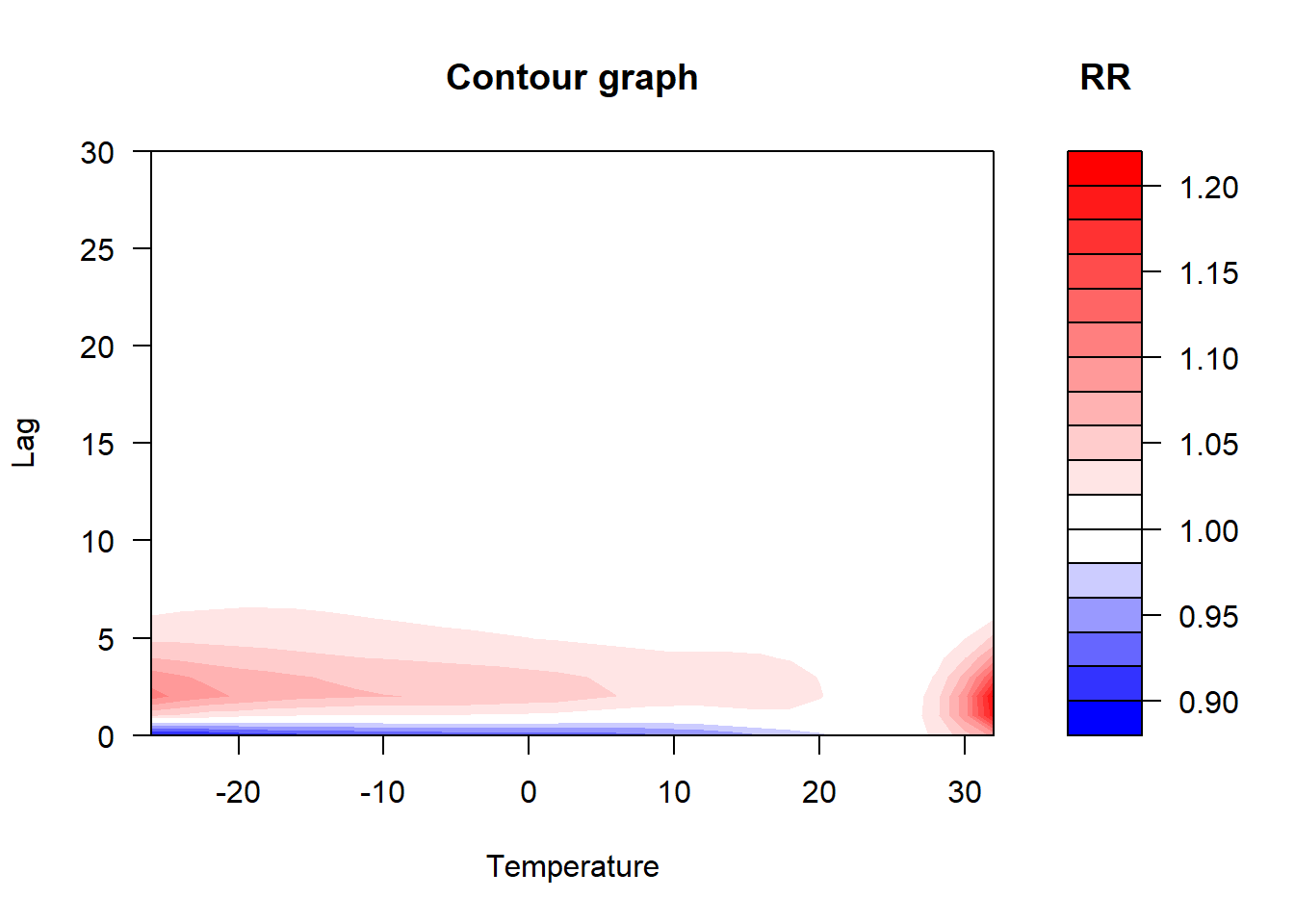
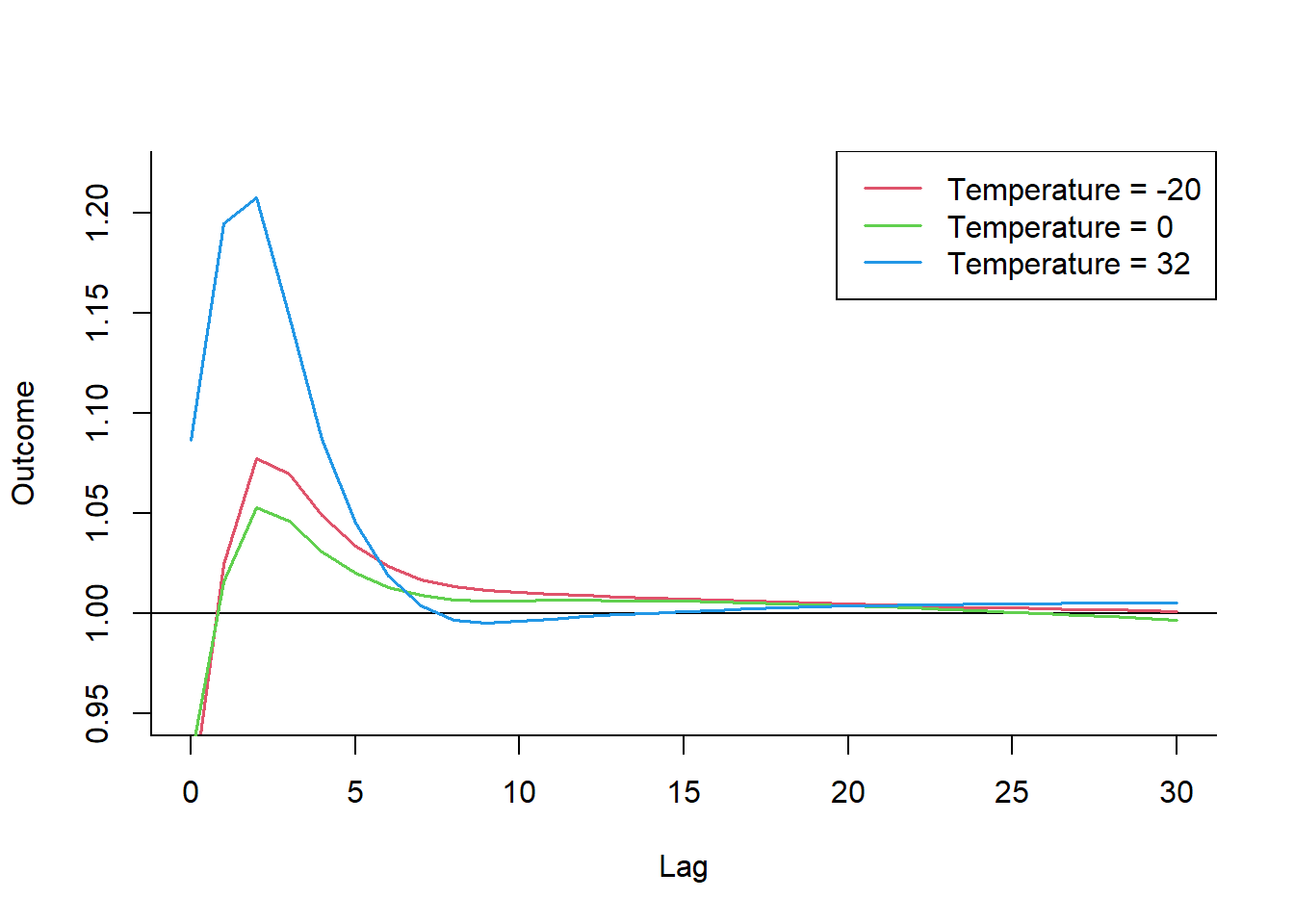
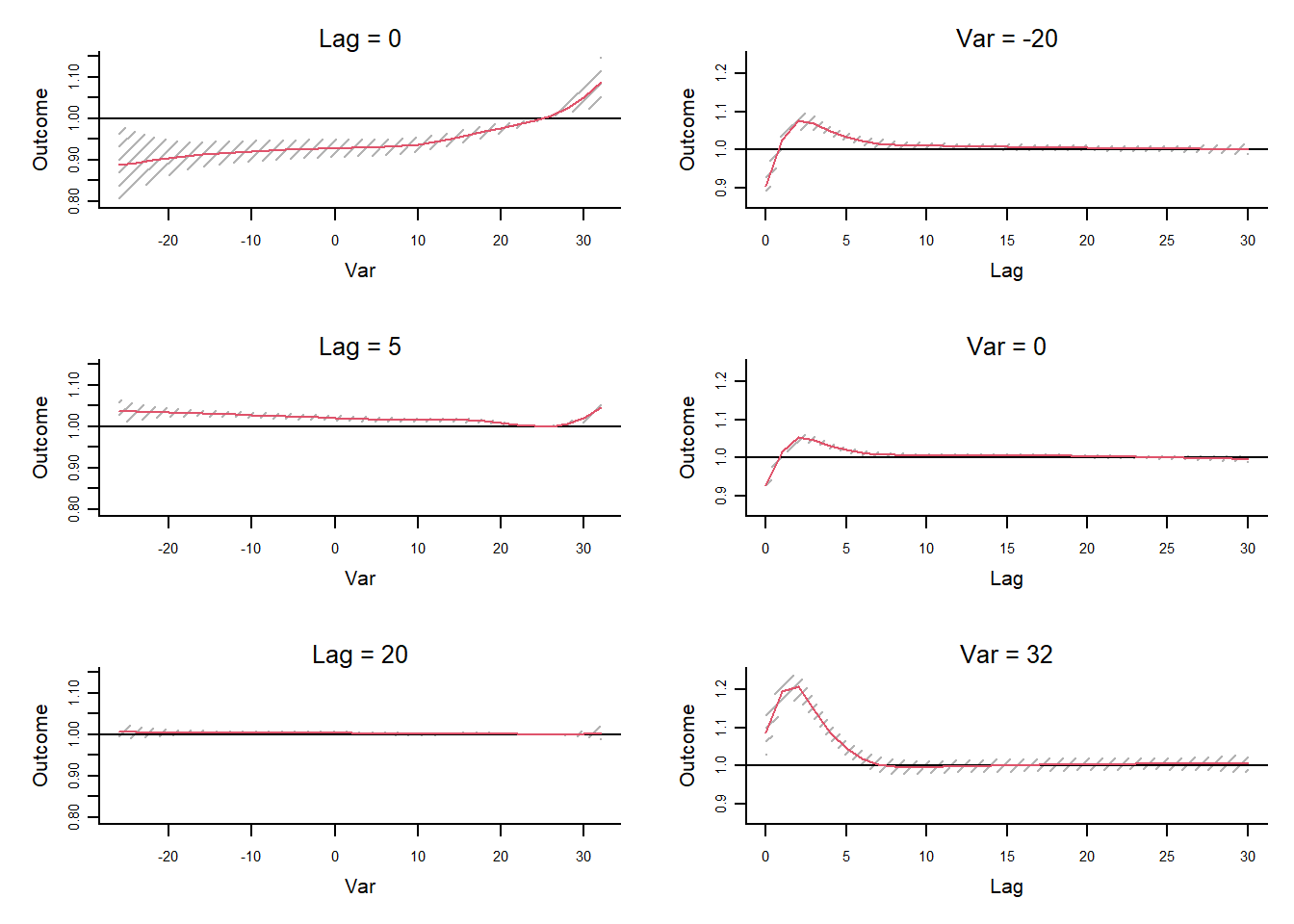
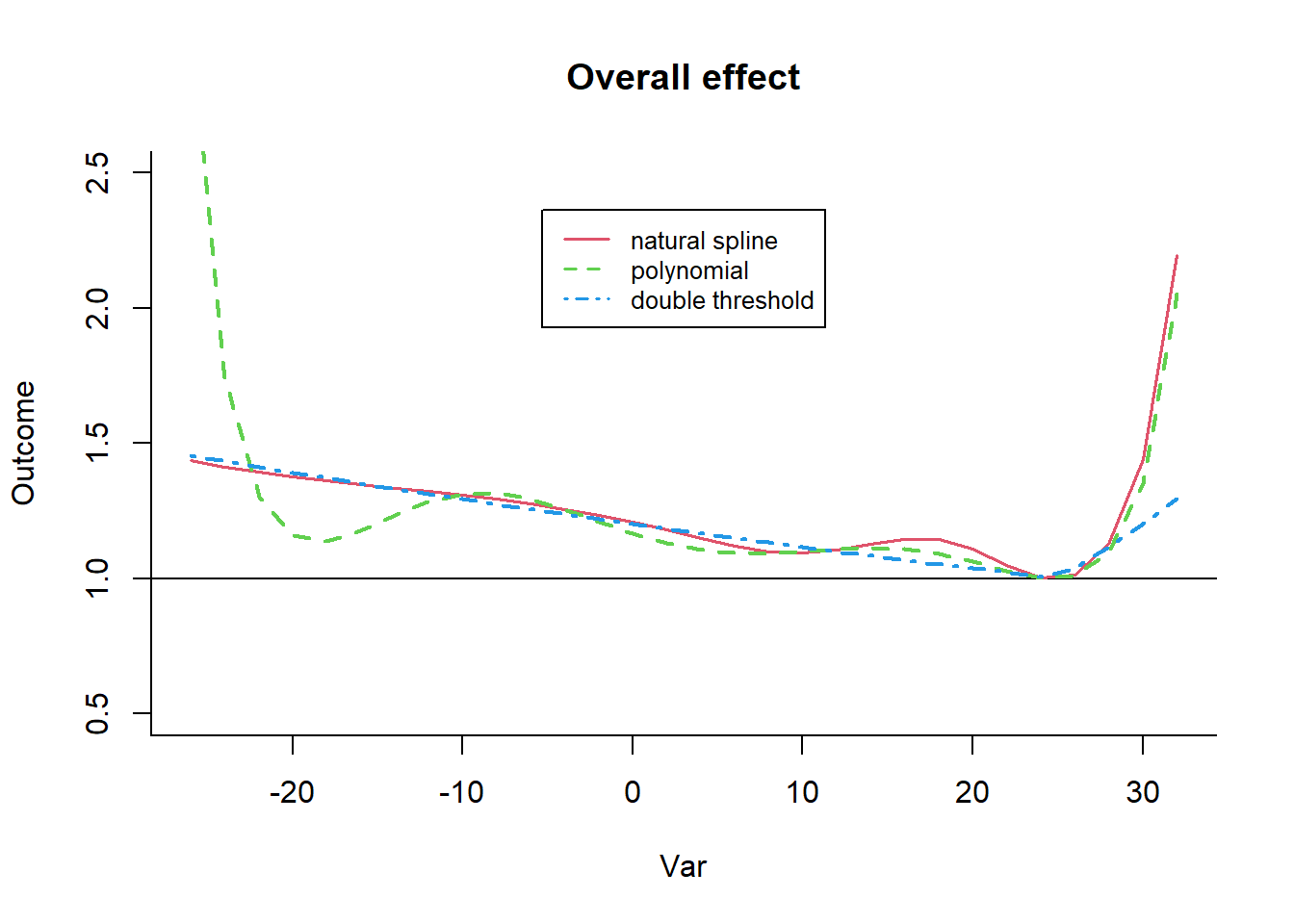
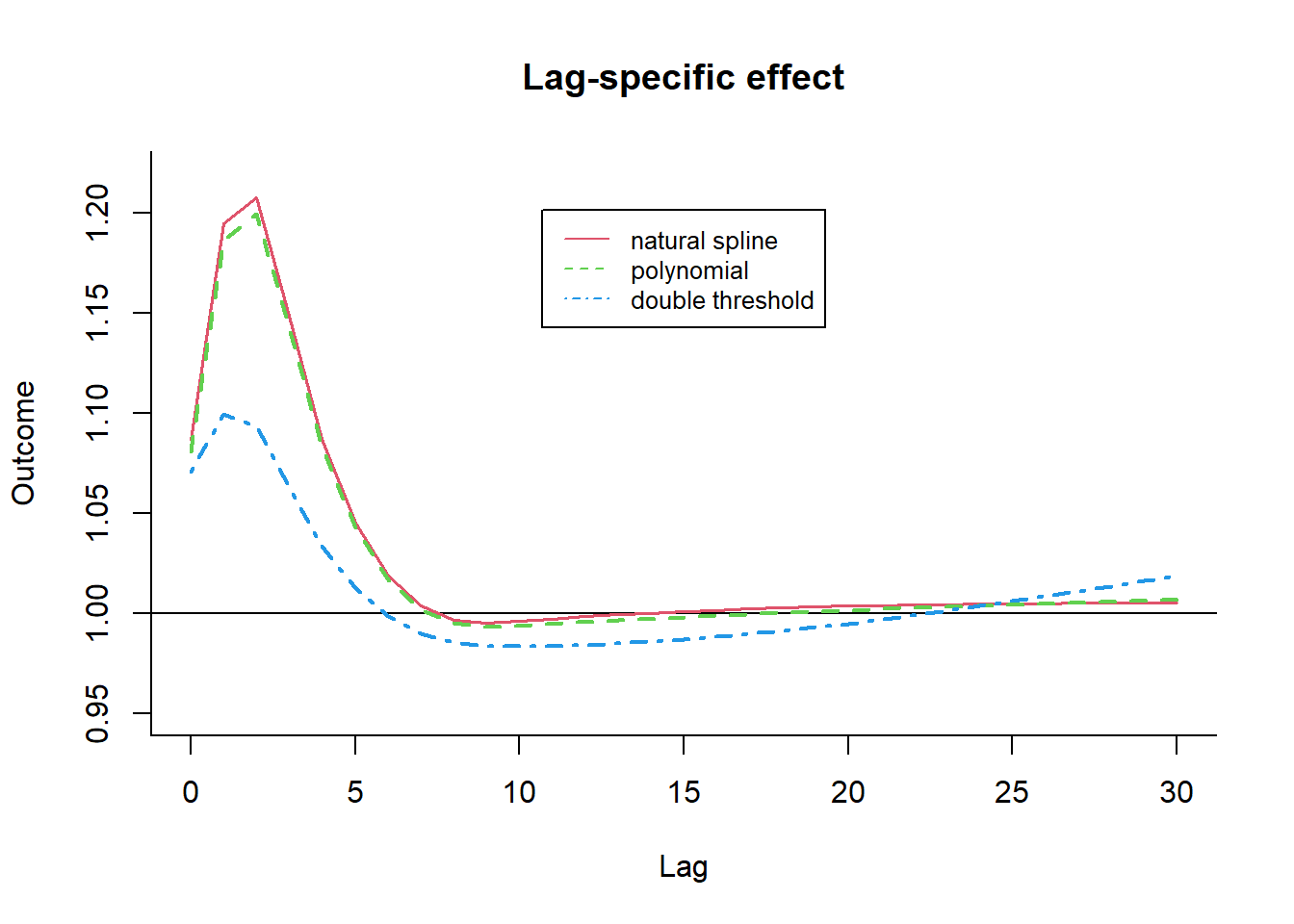
The bi-dimensional exposure-response relationship estimated by a DLNM may be difficult to summarize. The meaning of such parameters, which define the relationship along two dimensions, is not straightforward. Interpretation can be aided by the prediction of lag-specific effects on a grid of suitable exposure values and the L + 1 lags. In addition, the overall effects, predicted from exposure sustained over lags L to 0, can be computed by summing the lag-specific contributions.

Predicting from a DLNM

Predicted effects are computed in dlnm by the function crosspred(). The following code computes the prediction for ozone and temperature in the example:

pred.o3 <- crosspred(
  basis.o3,
  model,
  at = c(0:65, 40.3, 50.3)
) # chose the integers from 0 to 65 μgr/m3 in ozone, plus the value of the chosen threshold and 10 units above (40.3 and 50.3 μgr/m3, respectively)
pred.temp <- crosspred(
  basis.temp,
  model,
  by = 2, # rounded values within the temperature range with an increment of 2°C.
  cen = 25
)

The results stored in the crosspred object can be directly accessed to obtain specific figures or customized graphs other than those produced by dlnm plotting functions. For example, the overall effect for the 10-unit increase in ozone, expressed as RR and 95% confidence intervals, can be derived by:

pred.o3$allRRfit["50.3"] # RR = 1.05387
   50.3 
1.05387 
cbind(pred.o3$allRRlow, pred.o3$allRRhigh)["50.3", ] # combine low and high value
[1] 1.003354 1.106930
source(here("2-dlnm/dlnm_example.R"))
CROSSBASIS FUNCTIONS
observations: 5114 
range: -26.66667 to 33.33333 
lag period: 0 30 
total df:  30 

BASIS FOR VAR:
fun: bs 
knots: 1.666667 10.55556 19.44444 
degree: 3 
intercept: FALSE 
Boundary.knots: -26.66667 33.33333 

BASIS FOR LAG:
fun: ns 
knots: 1.105502 3.322105 9.983144 
intercept: TRUE 
Boundary.knots: 0 30

References

Gasparrini, Antonio. 2011. “Distributed Lag Linear and Non-Linear Models inR: The Packagedlnm.” Journal of Statistical Software 43 (8). https://doi.org/10.18637/jss.v043.i08.
Perperoglou, Aris, Willi Sauerbrei, Michal Abrahamowicz, and Matthias Schmid. 2019. “A Review of Spline Function Procedures in R.” BMC Medical Research Methodology 19 (1). https://doi.org/10.1186/s12874-019-0666-3.